case study questions on direct and inverse proportion class 8

• Direct and Inverse Proportions Class 8 Case Study Questions Maths Chapter 11

Last Updated on October 17, 2024 by XAM CONTENT

Hello students, we are providing case study questions for class 8 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 8 maths. In this article, you will find case study questions for CBSE Class 8 Maths Chapter 11 Direct and Inverse Proportions. It is a part of Case Study Questions for CBSE Class 8 Maths Series.

Table of Contents

Case Study Questions on Direct and Inverse Proportions

A hotel has 320 rooms and 32 cleaners to maintain them. With full capacity of staff, it took 2 hours to clean all the rooms.

Q. 1. On Monday 20% of the cleaners were not available. Will the cleaning of all rooms take more than 2 hours? How can you say so?

Difficulty Level: Easy

Sol. Yes. As, Number of man required to complete work is inversely proportional to time taken by them.

Q. 2. Ishan says, “The number cleaners available in the hotel is directly proportional to the time taken by them to clean the rooms.” Mira says, “The number of cleaners available in the hotel is inversely proportional to the time taken by them to clean the rooms.” Who is correct? Give reason.

Difficulty Level: Medium

Sol. Mira is correct, As Number of cleaners are inversely proportional to time taken

Q. 3. Equal number of rooms are allocated for each staff member for cleaning. How many rooms each cleaner had to maintain?

Sol. Number of rooms = 320 Number of cleaners = 32 Number of rooms cleaned by each cleaner = 320 / 32 = 10

Q. 4. The hotel administration hired 8 more cleaners. What is the change in number of rooms maintained by each cleaner?

Ans. Option (b) is correct. Explanation: Number of cleaners = 40 (32 + 8) Number of rooms cleaned by each cleaner = 320 / 40 = 8 So, Number of rooms decreased by (10 – 8) = 2

Q. 5. How many rooms has to be cleaned in an hour by each cleaner after the increase in the number of staff? ( (a) 1 (b) 4 (c) 8 (d) 10

Ans. Option (b) is correct. Explanation: Number of rooms to be cleaned in 2 hours = 8 Number of rooms to be cleaned in 1 hour = 8/2 = 4

• Lines and Angles Class 6 Case Study Questions Maths Chapter 2
• Patterns in Mathematics Class 6 Case Study Questions Maths Chapter 1
• Introduction to Graphs Class 8 Case Study Questions Maths Chapter 13
• Factorisation Class 8 Case Study Questions Maths Chapter 12
• Exponents and Powers Class 8 Case Study Questions Maths Chapter 10
• Mensuration Class 8 Case Study Questions Maths Chapter 9
• Algebraic Expressions and Identities Class 8 Case Study Questions Maths Chapter 8
• Comparing Quantities Class 8 Case Study Questions Maths Chapter 7
• Cube and Cube Roots Class 8 Case Study Questions Maths Chapter 6
• Square and Square Roots Class 8 Case Study Questions Maths Chapter 5
• Data Handling Class 8 Case Study Questions Maths Chapter 4
• Understanding Quadrilaterals Class 8 Case Study Questions Maths Chapter 3

Linear Equations in One Variable Class 8 Case Study Questions Maths Chapter 2

Rational numbers class 8 case study questions maths chapter 1, download ebooks for cbse class 8 maths.

• Rational Numbers Topicwise Worksheet for CBSE Class 8 Maths
• Linear Equations in One Variable Worksheet for CBSE Class 8 Maths
• Understanding Quadrilaterals Worksheet for CBSE Class 8 Maths
• Data Handling Worksheet for CBSE Class 8 Maths
• Squares and Square Roots Worksheet for CBSE Class 8 Maths
• Cube and Cube Roots Worksheet for CBSE Class 8 Maths
• Comparing Quantities Worksheet for CBSE Class 8 Maths
• Algebraic Expressions and Identities Worksheet for CBSE Class 8 Maths

Topics from which case study questions may be asked

• Direct Proportions
• Inverse Proportion

Whenever two quantities have a relation with each other such that if one changes, the other also changes then these quantities are said to be inter related with each other. This is called variation.

Example: (a) If number of something purchased increases then cost also increases. (b) If speed of vehicle increases, time taken decreases.

Quantities increasing or decreasing together need not be in direct proportion or indirect proportion.

Case study questions from the above given topic may be asked.

Frequently Asked Questions (FAQs) on Direct and Inverse Proportions Case Study

Q1: what is direct proportion.

A1: Direct proportion refers to a relationship between two quantities where an increase in one quantity leads to a proportional increase in the other, and a decrease in one result in a proportional decrease in the other. Mathematically, two quantities x and y are in direct proportion if x/y=k, where k is a constant.

Q2: What is inverse proportion?

A2: Inverse proportion describes a relationship between two quantities where an increase in one quantity leads to a proportional decrease in the other and vice versa. In this case, the product of the two quantities remains constant. Mathematically, two quantities x and y are in inverse proportion if x × y = k, where k is a constant.

Q3: How can I identify if two quantities are in direct proportion?

A3: – To identify if two quantities are in direct proportion, check if their ratio remains constant when they change. If the ratio of the two quantities stays the same, they are in direct proportion. For example, if 4 pencils cost ₹20, and 8 pencils cost ₹40, the ratio of pencils to price remains constant, indicating direct proportion.

Q4: How can I identify if two quantities are in inverse proportion?

A4: To determine if two quantities are in inverse proportion, check if the product of the two quantities remains constant when they change. If multiplying the two quantities always gives the same result, they are in inverse proportion. For example, if 4 workers take 6 days to complete a task, and 8 workers take 3 days, the product of workers and days (4 × 6 = 24 and 8 × 3 = 24) remains constant, indicating inverse proportion.

Q5: Can you give a real-life example of direct proportion?

A5: A common real-life example of direct proportion is the relationship between distance and time when speed is constant. If a car travels at a constant speed, doubling the time will double the distance covered, maintaining a constant ratio between distance and time.

Q6: Can you provide an example of inverse proportion in daily life?

A6: A typical example of inverse proportion is the relationship between the number of workers and the time taken to complete a task. If more workers are assigned to a job, the time required to finish the work decreases proportionally, assuming the work is equally distributed among the workers.

Q7: Why is learning about direct and inverse proportions important?

A7: Understanding direct and inverse proportions is crucial as these concepts are frequently used in real-life situations, such as calculating speed, cost, work efficiency, and more. Mastery of these concepts helps students develop problem-solving skills and apply mathematical relationships to practical problems.

Q8: Are there any online resources or tools available for practicing Direct and Inverse Proportions case study questions?

A8: We provide case study questions for CBSE Class 8 Maths on our  website . Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit  Physics Gurukul  website. they are having a large collection of case study questions for all classes.

Related Posts

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 8 Maths Chapter 13 Direct and Inverse Proportion

• Last modified on: 1 year ago
• Reading Time: 2 Minutes

Here we are providing Case Study questions for Class 8 Maths Chapter 13 Direct and Inverse Proportion.

Direct and Inverse Proportion Class 8 Maths Case Study Questions

Related posts, cbse class 8 maths chapter 13 direct and inverse proportion, learning outcomes, important keywords, download books – exam special.

Sample Papers for CBSE 2025 Exams

• Sample Question Papers for CBSE Class 8 All Subjects (for 2025 Exams)
• Sample Question Papers for CBSE Class 9 All Subjects (for 2025 Exams)
• Sample Question Papers for CBSE Class 10 All Subjects (for 2025 Exams)
• Sample Question Papers for CBSE Class 12 All Subjects (for 2025 Exams)

CBSE Class 10 Most Downloaded Books

• CBSE Important Numerical Problems Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Most Repeated Questions for Class 10 Science Board Exams

CBSE Class 12 Most Downloaded Books

• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Class 12 Physics Chapterwise Important Questions

CBSE Class 8 Most Downloaded Books

• Worksheets for CBSE Class 8 Maths – Chapterwise

ICSE Class 10

• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)
• ICSE Reasoning Based Questions Class 10 Geography BOARD Exams
• ICSE Revision Notes for Class 10 Chemistry BOARD Exams
• ICSE Revision Notes for Class 10 Physics BOARD Exams

ICSE Class 9

• ICSE Important Figure Based Questions Class 9 Physics Exams
• ICSE Important Numerical Problems for Class 9 Physics Exams
• ICSE Reasoning Based Questions Class 9 Geography BOARD Exams (150 Qs)

CBSE Chapter-Wise Test Papers

• CBSE Class 9 Science Chapterwise Test Papers
• CBSE Class 10 Science Chapterwise Test Papers
• CBSE Class 10 Maths Chapterwise Test Papers
• CBSE Class 10 Social Science Chapterwise Test Papers
• CBSE Class 12 Physics Chapterwise Test Papers
• CBSE Class 12 Chemistry Chapterwise Test papers

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

• School Solutions
• Star Program
• NCERT Solutions Class 12 Maths
• NCERT Solutions Class 12 Physics
• NCERT Solutions Class 12 Chemistry
• NCERT Solutions Class 12 Biology
• NCERT Solutions Class 12 Commerce
• NCERT Solutions Class 12 Economics
• NCERT Solutions Class 12 Accountancy
• NCERT Solutions Class 12 English
• NCERT Solutions Class 12 Hindi
• NCERT Solutions Class 11 Maths
• NCERT Solutions Class 11 Physics
• NCERT Solutions Class 11 Chemistry
• NCERT Solutions Class 11 Biology
• NCERT Solutions Class 11 Commerce
• NCERT Solutions Class 11 Accountancy
• NCERT Solutions Class 11 English
• NCERT Solutions Class 11 Hindi
• NCERT Solutions Class 11 Statistics
• NCERT Solutions Class 10 Maths
• NCERT Solutions Class 10 Science
• NCERT Solutions Class 10 English
• NCERT Solutions Class 10 Hindi
• NCERT Solutions Class 10 Social Science
• NCERT Solutions Class 9 Maths
• NCERT Solutions Class 9 Science
• NCERT Solutions Class 9 English
• NCERT Solutions Class 9 Hindi
• NCERT Solutions Class 9 Social Science
• NCERT Solutions Class 8 Maths
• NCERT Solutions Class 8 Science
• NCERT Solutions Class 8 English
• NCERT Solutions Class 8 Hindi
• NCERT Solutions Class 8 Social Science
• NCERT Solutions Class 7 Maths
• NCERT Solutions Class 7 Science
• NCERT Solutions Class 7 English
• NCERT Solutions Class 7 Hindi
• NCERT Solutions Class 7 Social Science
• NCERT Solutions Class 6 Maths
• NCERT Solutions Class 6 Science
• NCERT Solutions Class 6 English
• NCERT Solutions Class 6 Hindi
• NCERT Solutions Class 6 Social Science
• NCERT Solutions Class 5 Maths
• NCERT Solutions Class 5 English
• NCERT Solutions Class 5 EVS
• NCERT Solutions Class 4 Maths
• NCERT Solutions Class 4 English
• NCERT Solutions Class 4 EVS
• NCERT Solutions Class 4 Hindi
• NCERT Solutions Class 3 Maths
• NCERT Solutions Class 3 English
• NCERT Solutions Class 3 EVS
• NCERT Solutions Class 3 Hindi
• NCERT Solutions Class 2 Maths
• NCERT Solutions Class 2 English
• NCERT Solutions Class 2 Hindi
• NCERT Solutions Class 1 Maths
• NCERT Solutions Class 1 English
• NCERT Solutions Class 1 Hindi
• NCERT Books Class 12
• NCERT Books Class 11
• NCERT Books Class 10
• NCERT Books Class 9
• NCERT Books Class 8
• NCERT Books Class 7
• NCERT Books Class 6
• NCERT Books Class 5
• NCERT Books Class 4
• NCERT Books Class 3
• NCERT Books Class 2
• NCERT Books Class 1
• Important Questions Class 12
• Important Questions Class 11
• Important Questions Class 10
• Important Questions Class 9
• Important Questions Class 8
• Important Questions Class 7
• important questions class 6
• CBSE Class 12 Revision Notes
• CBSE Class 11 Revision Notes
• CBSE Class 10 Revision Notes
• CBSE Class 9 Revision Notes
• CBSE Class 8 Revision Notes
• CBSE Class 7 Revision Notes
• CBSE Class 6 Revision Notes
• CBSE Class 12 Syllabus
• CBSE Class 11 Syllabus
• CBSE Class 10 Syllabus
• CBSE Class 9 Syllabus
• CBSE Class 8 Syllabus
• CBSE Class 7 Syllabus
• CBSE Class 6 Syllabus
• CBSE Class 5 Syllabus
• CBSE Class 4 Syllabus
• CBSE Class 3 Syllabus
• CBSE Class 2 Syllabus
• CBSE Class 1 Syllabus
• CBSE Sample Question Papers For Class 12
• CBSE Sample Question Papers For Class 11
• CBSE Sample Question Papers For Class 10
• CBSE Sample Question Papers For Class 9
• CBSE Sample Question Papers For Class 8
• CBSE Sample Question Papers For Class 7
• CBSE Sample Question Papers For Class 6
• CBSE Sample Question Papers For Class 5
• CBSE Sample Question Papers For Class 4
• CBSE Sample Question Papers For Class 3
• CBSE Sample Question Papers For Class 2
• CBSE Sample Question Papers For Class 1
• CBSE Previous Year Question Papers Class 12
• CBSE Previous Year Question Papers Class 10
• Extra Questions For Class 8 Maths
• Extra Questions For Class 8 Science
• Extra Questions For Class 9 Maths
• Extra Questions For Class 9 Science
• Extra Questions For Class 10 Maths
• Extra Questions For Class 10 Science
• NEET 2021 Question Paper
• NEET 2020 Question Paper
• NEET 2019 Question Paper
• NEET 2018 Question Paper
• NEET 2017 Question Paper
• NEET 2016 Question Paper
• NEET 2015 Question Paper
• NEET Physics Questions
• NEET Chemistry Questions
• NEET Biology Questions
• NEET Sample Papers
• NEET Physics Syllabus
• NEET Chemistry Syllabus
• NEET Biology Syllabus
• NEET Mock Test
• NEET Eligibility Criteria
• JEE Main 2021 Question Paper
• JEE Main 2020 Question Paper
• JEE Main 2019 Question Paper
• JEE Main 2018 Question Paper
• JEE Main 2017 Question Paper
• JEE Main 2016 Question Paper
• JEE Main 2015 Question Paper
• JEE Main Sample Papers
• JEE Main Physics Syllabus
• JEE Main Chemistry Syllabus
• JEE Main Maths Syllabus
• JEE Main Physics Questions
• JEE Main Chemistry Questions
• JEE Main Maths Questions
• JEE main revision notes
• JEE Main Mock Test
• JEE Advanced Physics Questions
• JEE Advanced Chemistry Questions
• JEE Advanced Maths Questions
• JEE Advanced 2021 Question Paper
• JEE Advanced 2020 Question Paper
• JEE Advanced 2019 Question Paper
• JEE Advanced 2018 Question Paper
• JEE Advanced 2017 Question Paper
• JEE Advanced 2016 Question Paper
• JEE Advanced 2015 Question Paper
• JEE Advanced Physics Syllabus
• JEE Advanced Chemistry Syllabus
• JEE Advanced Maths Syllabus
• JEE Advanced Mock Test
• ISC Class 12 Syllabus
• ISC Class 11 Syllabus
• ICSE Class 10 Syllabus
• ICSE Class 9 Syllabus
• ICSE Class 8 Syllabus
• ICSE Class 7 Syllabus
• ICSE Class 6 Syllabus
• ISC Sample Question Papers for Class 12
• ISC Sample Question Papers for Class 11
• ICSE Sample Question Papers for Class 10
• ICSE Sample Question Papers for Class 9
• ICSE Sample Question Papers for Class 8
• ICSE Sample Question Papers for Class 7
• ICSE Sample Question Papers for Class 6
• ICSE Class 10 Revision Notes
• ICSE Class 9 Revision Notes
• ISC Important Questions for Class 12
• ISC Important Questions for Class 11
• ICSE Important Questions for Class 10
• ICSE Important Questions for Class 9
• ICSE Important Questions for Class 8
• ICSE Important Questions for Class 7
• ICSE Important Questions for Class 6
• ISC Class 12 Question Paper
• ICSE Class 10 Question Paper
• Maharashtra Board Syllabus
• Maharashtra Board Sample Question Paper
• Maharashtra Board Previous Year Question Paper
• AP Board Syllabus
• AP Board Sample Question Paper
• AP Board Previous Year Question Paper
• Tamilnadu Board Syllabus
• Tamilnadu Board Sample Question Paper
• Tamilnadu Board Previous Year Question Paper
• Telangana Board Syllabus
• Telangana Board Sample Question Paper
• Telangana Board Previous Year Question Paper
• Karnataka Board Syllabus
• Karnataka Board Sample Question Paper
• Karnataka Board Previous Year Question Paper
• Examination Full Forms
• Physics Full Forms
• Chemistry Full Forms
• Biology Full Forms
• Educational Full Form
• CUET Eligibility Criteria
• CUET Exam Pattern
• CUET Cutoff
• CUET Syllabus
• CUET Admit Card
• CUET Counselling
• CUET Previous Year Question Papers
• CUET Application Form
• CUET Sample Papers
• CUET Exam Centers
• CUET Exam Dates
• CUET Results
• Physics Formulas
• Chemistry Formulas
• Math Formulas
• Algebra Formulas
• Geometry Formulas
• Trigonometry Formulas
• Subscription

Important Questions Class 8 Maths Chapter 13

Home » CBSE » Important Questions Class 8 Maths Chapter 13

• CBSE Important Questions
• Important Questions Class 6
• CBSE Previous Year Question Papers
• CBSE Revision Notes
• CBSE Syllabus
• CBSE Extra Questions
• CBSE Sample Papers
• ISC & ICSE Syllabus
• ICSE Syllabus Class 9
• ICSE Syllabus Class 8
• ICSE Syllabus Class 7
• ICSE Syllabus Class 6
• ICSE Syllabus Class 10
• ICSE Question Paper
• ICSE Sample Question Papers
• ISC Sample Question Papers For Class 12
• ISC Sample Question Papers For Class 11
• ICSE Sample Question Papers For Class 10
• ICSE Sample Question Papers For Class 9
• ICSE Sample Question Papers For Class 8
• ICSE Sample Question Papers For Class 7
• ICSE Sample Question Papers For Class 6
• ICSE Revision Notes
• ICSE Important Questions
• ISC Important Questions For Class 12
• ISC Important Questions For Class 11
• ICSE Important Questions For Class 10
• ICSE Important Questions For Class 9
• ICSE Important Questions For Class 8
• ICSE Important Questions For Class 7
• ICSE Important Questions For Class 6
• Maharashtra board
• Rajasthan-Board
• Andhrapradesh Board
• AP Board syllabus
• Telangana Board
• Tamilnadu Board
• Tamilnadu Sample Question Paper
• Tamilnadu Syllabus
• Tamilnadu Previous Year Question Paper
• NCERT Solutions Class 12
• NCERT Solutions Class 10
• NCERT Solutions Class 11
• NCERT Solutions Class 9
• NCERT Solutions Class 8
• NCERT Solutions Class 7
• NCERT Solutions Class 6
• NCERT Solutions Class 5
• NCERT Solutions Class 4
• NCERT Solutions Class 3
• NCERT Solutions Class 2
• NCERT Solutions Class 1
• JEE Main Question Papers
• JEE Main Syllabus
• JEE Main Questions
• JEE Main Revision Notes
• JEE Advanced Question Papers
• JEE Advanced Syllabus
• JEE Advanced Questions
• JEE Advanced Sample Papers
• NEET Question Papers
• Neet 2021 Question Paper
• Neet 2020 Question Paper
• Neet 2019 Question Paper
• Neet 2018 Question Paper
• Neet 2017 Question Paper
• Neet 2016 Question Paper
• Neet 2015 Question Paper
• NEET Syllabus

Important Questions Class 8 Mathematics Chapter 13 – Direct and Indirect Proportions

Mathematics is one of the most engaging subjects, which requires students of all classes to engross themselves in the concepts and hypotheses relevant to the subject. Class 8 Mathematics Chapter 13 is about Direct and Indirect Proportion. It is one of the most crucial topics in Mathematics. Following are the topics covered in this chapter:

Quick Links

• Introduction
• Direct Proportion
• Inverse Proportion

The official website of Extramarks is here to provide students with a clear and elaborate understanding of concepts, hypotheses, significant questions, NCERT book solutions and many other critical examples.

Sedulous practice on a regular basis is the only way to score excellent marks. Extramarks is a very trustworthy platform that has guided and supported lakhs of students in their exam preparation.. Our team understands the value of regularly solving complex problems when it comes to Mathematics. After carefully researching and analysing CBSE past year question papers, NCERT books, and exemplars, our highly qualified and experienced professionals have come up with the question bank Important Questions Class 8 Mathematics Chapter 13 for the students. Students can take help from our question bank Important Questions Class 8 Mathematics Chapter 13 to practise some fundamental questions relevant to the chapter Direct and Indirect Proportion so they can practice well and maximise their potential and excel in their examinations. 

Along with providing Important Questions Class 8 Chapter 13, our Extramarks website also provides the students with the CBSE revision notes, the CBSE sample papers, and CBSE past year question papers that strictly adhere to the latest CBSE syllabus.

Get Access to CBSE Class 8 Maths Important Questions 2022-23 with Chapter-Wise Solutions

You can also find CBSE Class 8 Maths Chapter-by-Chapter Important Questions here:

Direct and Inverse Proportion Class 8 Extra क़ुएस्तिओन्स – With Solutions

Given  below are some of the  important questions and their solutions covered in our Chapter 13 Class 8 Mathematics Important Questions:

Question 1: A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?

Answer 1: Let the number of bottles filled in 5 hours = x

We can see that here the ratio of hours and bottles are in direct proportion.

6/840 = 5/x

=⟩ 6x = 840 × 5

=⟩ x = (840 × 5) / 6

Therefore, the machine will fill up 700 bottles in 5 hours.

Question 2: Suppose 2 kg of sugar contains 9 × 10 6 crystals. How many sugar crystals are there in

(i) 5kg of sugar?

(ii) 1.2 kg of sugar?

Answer 2: (i) Let the number of sugar crystals = x

We can see that the weight of sugar and the number of crystals are directly proportional.

2/(9 × 10 6 ) = 5/x

=⟩ 2x = 9 × 10 6 × 5

=⟩ x = (9 × 10 6 × 5)/2

=⟩ x = 2.25 × 10 7 

Therefore, there are 2.25 × 10 7 crystals.

(ii) Let the number of sugar crystals = x

Now, we can see that the weight of sugar and the number of crystals are directly proportional.

2/(9 × 10 6 ) = 1.2/x

=⟩ 2x = (1.2 × 9 × 10 6 )

=⟩ x = (1.2 × 9 × 10 6 ) / 2 = 5.4 × 10 6

Therefore, the number of sugar crystals in 1.2 kg sugar is 5.4 × 10 6 

Question 3: A 5m 60cm high vertical pole casts a shadow which is 3m 20cm long. Find at the same time

(i) length of the shadow cast by a different pole which is 10m 50cm high.

(ii) height of a pole which casts a shadow 5m long.

Answer 3: Here, we can see that the pole’s height and the shadow’s length are directly proportional.

And we know that 1m = 100cm

Hence, 5m 60cm = 5 × 100 + 60 = 560cm

3m 20cm = 3 × 100 + 20 = 320cm

10m 50cm = 10 × 100 + 50 = 1050cm

5m = 5 × 100 = 500cm

(i) Let the length of the shadow of another pole = x

560/320 = 1050/x

=⟩ x × 560 = 1050 × 320

=⟩ x = (1050 × 320)/560

=⟩ x = 600cm = 6m

Therefore, the length of the shadow of another pole is 6m.

(ii) Let the height of the pole = x

560/320 = x/500

=⟩ x × 320 = 560 × 500

=⟩ x = (560 × 500)/320

=⟩ x = 875cm = 8.75m 

Therefore, the height of the pole is 8.75m 

Question 4: In a Television game show, total prize money of Rs. 1,00,000 has to be divided equally among the winners. Complete the below table and find out whether the prize money given to one individual winner is directly or inversely proportional to the total number of winners:

Answer 4: Here, we can see that the number of winners and prize money are inversely proportional because winners are increasing, prize money is decreasing.

When the number of winners is 4, the winner will receive = 100000/4 = Rs. 25000

When the number of winners is 5, the winner will receive = 100000/5 = Rs. 20000

When the number of winners is 8, the winner will receive = 100000/8 = Rs. 12500

When the number of winners is 10, the winner will receive = 100000/10 = Rs. 10000

When the number of winners is 20, the winner will receive = 100000/20 = Rs. 5000

Question 5: Rehman is making a wheel using spokes. He wants to fix equal spokes so that the angles between any pair of consecutive spokes are equal. Help him by completing the following table.

(i) Are the number of spokes and the angles formed between the pairs of consecutive spokes inversely proportional?

(ii) Find out the angle between a pair of consecutive spokes on a wheel with 15 spokes.

(iii) If the angle between a pair of consecutive spokes is 40 degrees, how many spokes would be needed?

Answer 5: Here, we can see that the number of spokes is inversely proportional to the angle between the pair of consecutive spokes as the number of spokes increases and the angle between the pair of consecutive spokes decreases. 

And we know that the centre of a circle is 360°.

When the number of spokes is 8, then the angle between the pair of consecutive spokes = 360/8 = 45°

And when the number of spokes is 10, then the angle between a pair of consecutive spokes = 360/10 = 36°

And when the number of spokes is 12, then the angle between a pair of consecutive spokes = 360/12 = 30°

(i) Yes. The number of spokes is inversely proportional to the angle between a pair of consecutive spokes.

(ii) When the number of spokes is 15, the angle between the pair of consecutive spokes = 360/15 = 24°

(iii) Number of spokes needed if the angle between the pair of consecutive spokes is 40° = 360/40 = 9

Question 6: A contractor estimates that 3 persons could rewire Jasminder’s house in 4 days. If he uses 4 persons instead of three, how long should they take to complete the job?

Solution: Let the time it takes to complete the job = x

Here, we can see that the number of persons and days are inversely proportional.

Therefore, 3/4 = x/4

=⟩ 3 × 4 = 4x

=⟩ x = 12/4 = 3

Hence, 4 persons will require 3 days to complete the work.

Question 7: A factory requires 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?

Answer 7: Let the number of required machines = x

Here, the number of machines are inversely proportional to the number of days.

Therefore, 63/54 = x/42

=⟩ 63 × 42 = 54x

=⟩ x = (63 × 42)/54

Hence, 49 machines are required for 54 days.

Question 8: Two people  could fit new windows in a house in 3 days.

(i) One of the persons fell ill before the work started. How long would the job take now?

(ii) How many people  would be needed to fit the windows in one day?

Answer 8: Let the number of days = x

Here, the number of persons is inversely proportional to the number of days.

Therefore, 6 days are required by 1 person to complete the job.

(ii) Let the number of persons = x

Therefore, 6 persons are required to complete the work in 1 day.

Question 9: Under the condition that the temperature remains constant, the volume of gas is inversely proportional to its pressure. If the volume of gas is 630 cubic centimetres at a pressure of 360 mm of mercury, then what will be the pressure of the gas if its volume is 720 cubic centimetres at the same temperature?

Answer 9: Given that, at a constant temperature, the pressure and volume of a gas are inversely proportional. 

Let the pressure = x

630/720 = x/360

=⟩ x =  (630 × 360)/720 

=⟩ x = 315 mm of mercury

Hence, 315 mm of mercury will be the pressure of 720 cc gas.

Question 10: A contractor undertook a contract to complete a part of a stadium in 9 months with a team of 560 persons. Later on, it was required to complete the job in 5 months. How many extra persons should be employed to complete the work?

Answer 10: Here, we can see that the number of persons is inversely proportional to the number of months.

Hence, Let the number of persons required = x

Therefore, 560/x = 5/9

=⟩ 5x = 560 × 9

=⟩ x = 5040/5

=⟩ x =1008 

We know that 1008 persons are required to complete the work in 5 months.

Therefore, the number of extra persons required = 1008 – 560 = 448 persons

Hence, the 448 extra persons are required to complete the work in 5 months.

Benefits of Solving Important Questions Class 8 Mathematics Chapter 13

When it comes to Mathematics, practice is mandatory for a student to gain mastery in this subject. Only thorough practice can help students get a good hold of the concepts and feel confident in Mathematics. By practising the Important Questions Class 8 Mathematics Chapter 13 provided on the website of Extramarks, students prepare themselves properly for their examinations.

Below are some benefits of solving Class 8 Mathematics Chapter 13 Important Questions:

• Important Questions Class 8 Mathematics Chapter 13 is a set of carefully selected questions by experienced Mathematics faculty members. Our experts have prepared these questions after considering the past years’  question papers  and examining several CBSE textbooks. 
• Every question and answer provided by Mathematics Class 8 Chapter 13 Important Questions strictly adheres to the latest CBSE syllabus and follows the latest CBSE guidelines so that the students can completely rely on the solutions provided by the website. 
• All the Chapter 13 Class 8 Mathematics Important Questions have been solved and supported with the required formulas and explanations for the students to understand the concept well and overall clarification. 
• Students can trust and enjoy the process of learning help to speed up their learning and improve their academic performance, through revisions and make them aware of their mistakes through guided practice and help to get the best results

Along with Important Questions, Class 8 Mathematics Chapter 13, the online learning platform Extramarks also provides the following:

• NCERT books 
• CBSE revision notes 
• CBSE sample paper 
• Important Formulas 
• CBSE past years’ question papers
• CBSE extra questions
• Click to share on Facebook (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on WhatsApp (Opens in new window)

Q.1 If 56 men can do a piece of work in 42 days, how many men are required to complete it in 14 days

Marks: 3 Ans

Let x no. of men are required to complete the work in 14 days.

56 × 42 = x × 14 x = 56 × 42 14 = 168

Therefore, 168 men are required to complete the work in 14 days.

Q.2 A garrison of 500 men had provision for 24 days. However, a reinforcement of 300 men arrived. How long the food will last

Marks: 2 Ans

Let the number of days the food last for 500 + 300 = 800 men be x.

500 × 24 = 800 × x x = 500 × 24 800 = 15 days.

Therefore, the food will last for 15 days.

Q.3 The scale of a map is given as 1 : 40000000. Two cities are 4 cm apart on the map. Find the actual distance between them.

Let the map distance be x cm and the actual distance be y cm. Then,

1 : 40000000 = x : y

1 4 — 10 7 = x y 1 4 — 10 7 = 4 y y = 16 — 10 7 cm or y = 1600 km

Two cities which are 4 cm apart on the map are actually 1600 km away from each other.

Q.4 If 9 kg of rice costs 166.50, how much rice can be purchased for 259

Marks: 1 Ans

Let x kg rice can be purchased for 259. Then,

166 .50 9 = 259 x x = 9 × 259 166 .5 = 14 kg. 14kg rice can be purchased for 259.

Q.5 A car can finish a journey in 10 hours at the speed of 48 km/hr. By how much should its speed be increased so that it may take only 8 hours to cover the same distance

Let the speed be x km/hr for covering the same distance in 8 hours.

48 — 10 = 8 — x x= 48 — 10 8 = 60 km/hours

Therefore, the speed needs to be increased by 12 km/hr.

Please register to view this section

Cbse class 8 maths important questions, chapter 1 - rational numbers.

Chapter 2 - Linear Equations in One Variable

Chapter 3 - understanding quadrilaterals, chapter 4 - practical geometry, chapter 5 - data handling, chapter 6 - squares and square roots, chapter 7 - cubes and cube roots, chapter 8 - comparing quantities, chapter 9 - algebraic expressions and identities, chapter 10 - visualising solid shapes, chapter 11 - mensuration, chapter 12 - exponents and powers, chapter 14 - factorisation, chapter 15 - introduction to graphs, chapter 16 - playing with numbers, faqs (frequently asked questions), 1. what are the topics covered in important questions class 8 mathematics chapter 13.

Our expert Mathematics faculty members have carefully chosen some  significant question bank Important Questions Class 8 Mathematics Chapter 13. The questions have been picked after carefully analysing and discussing all the important CBSE past year question papers, NCERT books and exemplars. The questions in our question bank cover the following topics:

• Inverse Proportion.

2. How will Important Questions Class 8 Mathematics Chapter 13 help the students score well in their examinations?

Mathematics requires students to practice on a regular basis for them to get a good command over the concepts. Deciphering problems and doing self-assessment about their strong and weak areas  is an effective approach to gain mastery in Mathematics.

Students can completely trust and rely on the Extramarks question bank, such as Important Questions Class 8 Mathematics Chapter 13, to get an idea about exam-related questions and their solutions. Our professionals have picked up some constructive questions after thoroughly analysing and considering the CBSE past year’s question papers. Students solving these questions on a regular basis can get excellent results in their exams.

3. Which are the chapters covered in CBSE Class 8 Mathematics syllabus?

Many important chapters that form the fundamentals  of Class 10 Mathematics are there in Class 8 Mathematics syllabus. Given below is a complete list of these 16 chapters:

• Chapter 1- Rational Numbers
• Chapter 2 – Linear Equations in One Variable
• Chapter 3 – Understanding Quadrilaterals
• Chapter 4 – Practical Geometry
• Chapter 5 – Data Handling
• Chapter 6 – Square and Square Roots
• Chapter 7 – Cube and Cube Roots
• Chapter 8 – Comparing Quantities
• Chapter 9 – Algebraic Expressions and Identities
• Chapter 10 – Visualising Solid Shapes
• Chapter 11- Mensuration
• Chapter 12 – Exponents and Powers
• Chapter 13 – Direct and Inverse Proportions
• Chapter 14 – Factorisation
• Chapter 15 – Introduction to Graphs
• Chapter 16 – Playing with Numbers

CBSE Related Links

Fill this form to view question paper

Otp verification.

• CBSE- Direct and Inverse Proportions
• Sample Papers

Direct and Inverse Proportions-Sample Papers

• STUDY MATERIAL FOR CBSE CLASS 8 MATH
• Chapter 1 - Algebraic Expressions and Identities
• Chapter 2 - Comparing Quantities
• Chapter 3 - Cubes and Cube Roots
• Chapter 4 - Data handling
• Chapter 5 - Direct and Inverse Proportions
• Chapter 6 - Exponents and Powers
• Chapter 7 - Factorization
• Chapter 8 - Introduction to Graphs
• Chapter 9 - Mensuration
• Chapter 10 - Playing with Numbers
• Chapter 11 - Practical Geometry
• Chapter 12 - Squares and Square Roots
• Chapter 13 - Visualizing Solid Shapes
• Chapter 14 - Linear Equations in One Variable
• Chapter 15 - Rational Numbers
• Chapter 16 - Understanding Quadrilaterals

• NCERT Solutions
• NCERT Class 8
• NCERT 8 Maths
• Chapter 13: Direct Inverse Proportions

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions

Ncert solutions class 8 maths chapter 13 – free pdf download.

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions is designed with the aim of helping students practise more and more questions and clear their doubts related to the concepts and topics in this chapter. Set of CBSE Class 8 Maths questions has been structured and answered in an easy and logical manner, using step-by-step problem-solving techniques.

Download Exclusively Curated Chapter Notes for Class 8 Maths Chapter – 13 Direct and Inverse Proportions

Download most important questions for class 8 maths chapter – 13 direct and inverse proportions.

For more practice, find below the free PDF of Maths NCERT Class 8 Solutions designed by subject experts at BYJU’S, as per the latest  CBSE curriculum. A direct and inverse proportion are applied to determine how the quantity and amount are correlated with each other. They are also designated as directly proportional or inversely proportional. ‘∝’ is the symbol used to denote proportionality. For instance, if a is proportional to b, then it is represented as ‘a∝b’. On the other hand, if a is inversely proportional to b, then it is denoted as ‘a∝1/b’. The concepts can be grasped well using the NCERT Solutions at BYJU’S.

carouselExampleControls112

Previous Next

Access Answers to NCERT Class 8 Maths Chapter 13 Direct and Inverse Proportions

Exercise 13.1 page no: 208.

1. The following are the car parking charges near a railway station up to,

4 hours – Rs.60

8 hours – Rs.100

12 hours – Rs.140

24 hours – Rs.180

Check if the parking charges are in direct proportion to the parking time.

Charges per hour:

C1 = 60/4 = Rs. 15

C2 = 100/8 = Rs. 12.50

C3 =  140/12 = Rs. 11.67

C4 = 180/24  = Rs.7.50

Here, the charges per hour are not the same, i.e. C1 ≠ C2 ≠ C3 ≠ C4

Therefore, the parking charges are not in direct proportion to the parking time.

2. A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of the base. In the following table, find the parts of the base that need to be added.

Let the ratio of parts of red pigment and parts of the base be a/b.

Case 1: Here, a 1 = 1, b 1 = 8

a 1 /b 1 = 1/8 = k (say)

Case 2: When  a 2 = 4, b 2 =?

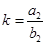
b 2 = a 2 /k = 4/(1/8) = 4×8 = 32

Case 3: When  a 3 = 7, b 3 =?

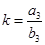
b 3 = a 3 /k = 7/(1/8) = 7×8 = 56

Case 4: When a 4 = 12, b 4 =?

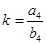
b 4 = a 4 /k = 12/(1/8) = 12×8 = 96

Case 5: When  a 5 = 20, b 5 =?

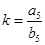
b 5 = a 5 /k = 20/(1/8) = 20×8 = 160

When combining results for all the cases, we get

3. In Question 2 above, if 1 part of a red pigment requires 75 mL of the base, how much red pigment should we mix with 1800 mL of the base?

Let the parts of red pigment mix with 1800 mL base be x.

Since it is in direct proportion,

Hence, with the base 1800 mL, 24 parts of the red pigment should be mixed.

4. A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?

Let the number of bottles filled in five hours be x.

Here, the ratio of hours and bottles is in direct proportion.

x = 5×840/6 = 700

Hence, the machine will fill 700 bottles in five hours.

5. A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm, as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?

Let the enlarged length of bacteria be x.

Actual length of bacteria = 5/50000 = 1/10000  cm = 10 -4  cm

Here, the length and enlarged length of bacteria are in direct proportion.

Hence, the enlarged length of bacteria is 2 cm.

6. In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?

Let the length of the model ship be x.

Here, the length of the mast and the actual length of the ship are in direct proportion.

Hence, the length of the model ship is 21 cm.

7. Suppose 2 kg of sugar contains 9×10 6 crystals. How many sugar crystals are there in

(i) 5 kg of sugar? (ii) 1.2 kg of sugar?

(i) Let sugar crystals be x.

Here, the weight of sugar and the number of crystals are in direct proportion.

(ii)  Let sugar crystals be x.

Hence, the number of sugar crystals is  5.4×10 6 .

8. Rashmi has a road map with a scale of 1 cm representing 18 km. She drives on the road for 72 km. What would be her distance covered on the map?

Let the distance covered in the map be x.

Here, the actual distance and distance covered in the map are in direct proportion.

Hence, the distance covered on the map is 4 cm.

9. A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time (i) the length of the shadow cast by another pole 10 m 50 cm high (ii) the height of a pole which casts a shadow 5 m long.

Here, the height of the pole and the length of the shadow are in direct proportion.

And 1 m = 100 cm

5 m 60 cm = 5×100+60 = 560 cm

3 m 20 cm = 3×100+20 = 320 cm

10 m 50 cm = 10×100+50 = 1050 cm

5 m = 5×100 = 500 cm

(i) Let the length of the shadow of another pole be x.

x= 600 cm = 6m

Hence, the length of the shadow of another pole is 6 m.

(ii) Let the height of the pole be x.

= 875 cm = 8 m 75 cm

Hence, the height of the pole is 8 m 75 cm.

10. A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?

Let the distance covered in 5 hours be x km.

1 hour = 60 minutes

Therefore, 5 hours = 5×60 = 300 minutes

Here, the distance covered and time are in direct proportion.

Therefore, the truck can travel 168 km in 5 hours.

Exercise 13.2 Page No: 213

1. Which of the following are in inverse proportion?

(i) The number of workers on a job and the time to complete the job.

(ii) The time taken for a journey and the distance travelled at a uniform speed.

(iii) Area of cultivated land and the crop harvested.

(iv) The time taken for a fixed journey and the speed of the vehicle.

(v) The population of a country and the area of land per person.

(i) The number of workers and the time to complete the job is in inverse proportion because less workers will take more time to complete a job, and more workers will take less time to complete the same job.

(ii) Time and distance covered in direct proportion.

(iii) It is a direct proportion because more are of cultivated land will yield more crops.

(iv) Time and speed are in inverse proportion because if time is less, speed is more.

(v) It is an inverse proportion. If the population of a country increases, the area of land per person decreases.

2. In a Television game show, the prize money of Rs.1,00,000 is to be divided equally amongst the winners. Complete the following table and find whether the prize money given to an individual winner is directly or inversely proportional to the number of winners:

Here, the number of winners and prize money are in inverse proportion because winners are increasing, and prize money is decreasing.

When the number of winners is 4, each winner will get =100000/4 = Rs. 25,000

When the number of winners is 5, each winner will get =100000/5 = Rs. 20,000

When the number of winners is 8, each winner will get =100000/8 = Rs. 12,500

When the number of winners is 10, each winner will get = 100000/10 = Rs. 10,000

When the number of winners is 20, each winner will get = 100000/20 = Rs. 5,000

3. Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table:

(i) Are the number of spokes and the angles formed between the pairs of consecutive spokes in inverse proportion?

(ii) Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes.

(iii) How many spokes would be needed, if the angle between a pair of consecutive spokes is 40 degree?

Here, the number of spokes is increasing, and the angle between a pair of consecutive spokes is decreasing. So, it is an inverse proportion, and the angle at the centre of a circle is 360 degree.

When the number of spokes is 8, then the angle between a pair of consecutive spokes = 360/8 = 45 degree

When the number of spokes is 10, then the angle between a pair of consecutive spokes = 360/10= 36 degree.

When the number of spokes is 12, then the angle between a pair of consecutive spokes = 360/12 = 30 degree.

(i) Yes, the number of spokes and the angles formed between a pair of consecutive spokes is in inverse proportion.

(ii) When the number of spokes is 15, then the angle between a pair of consecutive spokes = 360/15= 24 degree.

(iii) The number of spokes would be needed = 360/40 = 9

4. If a box of sweets is divided among 24 children, they will get 5 sweets each. How many would each get, if the number of children is reduced by 4?

Each child gets = 5 sweets

24 children will get 24×5 = 120 sweets.

Total number of sweets = 120

If the number of children is reduced by 4, then children left = 24-4 = 20

Now, each child will get sweets = 120/20 = 6 sweets

5. A farmer has enough food to feed 20 animals in his cattle for 6 days. How long would the food last if there were 10 more animals in his cattle?

Let the number of days be x.

Total number of animals = 20+10 = 30

Here, the number of animals and the number of days are in inverse proportion.

Hence, the food will last for four days.

6. A contractor estimates that 3 persons could rewire Jasminder’s house in 4 days. If he uses 4 persons instead of three, how long should they take to complete the job?

Let the time taken to complete the job be x.

Here, the number of persons and the number of days are in inverse proportion.

Hence, 4 persons will complete the job in 3 days.

7. A batch of bottles was packed in 25 boxes, with 12 bottles in each box. If the same batch is packed using 20 bottles in each box, how many boxes would be filled?

Let the number of boxes be x.

Here, the number of bottles and the number of boxes are in inverse proportion.

12/20 = x/25

12×25 = 20x

x = 12×25/20 = 15

Hence, 15 boxes would be filled.

8. A factory requires 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?

Let the number of machines required be x.

Here, the number of machines and the number of days are in inverse proportion.

63/54 = x/42

63×42 = 54x

x = 63×42/54

Hence, 49 machines would be required.

9. A car takes 2 hours to reach a destination by travelling at the speed of 60 km/hr. How long will it take when the car travels at the speed of 80 km/hr?

Let the number of hours be x.

Here, the speed of the car and time are in inverse proportion.

60/80 = x/2

x = 60×2/80

10. Two persons could fit new windows in a house in 3 days.

(i) One of the persons fell ill before the work started. How long would the job take now?

(ii) How many persons would be needed to fit the windows in one day?

(i) Let the number of days be x.

(ii) Let the number of persons be x.

x = 6 persons

11. A school has 8 periods a day, each of 45 minutes duration. How long would each period be, if the school has 9 periods a day, assuming the number of school hours to be the same?

Let the duration of each period be x.

Here, the number of periods and the duration of periods are in inverse proportion.

Hence, the duration of each period would be 40 minutes.

Class 8 Mathematics NCERT Solutions are provided with a wide range of exercises based on the CBSE syllabus. This learning resource helps Class 8 students to clear their doubts and get ready for the annual exam. In Class 8 CBSE Chapter 13, students will see how variation in one quantity brings variation in the other quantity, basic concepts of variation, for example, more the money deposited in a bank, the more the interest earned.

NCERT Solutions for Class 8 Maths Chapter 13 Exercises

Get the detailed solutions for all the questions listed under the below exercises:

Exercise 13.1 Solutions : 10 Questions (Short answers)

Exercise 13.2 Solutions : 11 Questions (Long answers)

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions Summary

The NCERT Solutions for Class 8 Maths deals primarily with the solutions for the major problems associated with the topic of direct and inverse proportions. Class 8 NCERT Maths , Chapter 13 – Direct and Inverse Proportions introduce the concept of direct proportion, inverse proportion, their properties and real-life applications.

The main topics covered in this chapter include the following:

Key Features of NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions

• These NCERT solutions are an easy way to practise and learn the concepts.
• Simple and easy language is used.
• Subject experts have consolidated all exercise questions in one place for practice.
• All solutions are designed using a step-by-step problem-solving approach.
• NCERT Solutions are helpful for the preparation of competitive exams.

Frequently Asked Questions on NCERT Solutions for Class 8 Maths Chapter 13

What is the use of practising ncert solutions for class 8 maths chapter 13, can the ncert solutions for class 8 maths chapter 13 be viewed offline, list out the topics of ncert solutions for class 8 maths chapter 13., leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Class 6th Science
• Class 7th Science
• Class 8th Science
• Class 9th Science
• Class 10th Science
• Life-like 3D Videos
• Augmented Reality
• Virtual Reality

Direct and Inverse Proportions

13.1 INTRODUCTION Mohan prepares tea for himself and his sister. He uses 300 ml of water, 2 spoons of sugar, 1 spoon of tea leaves and 50 ml of milk. 

How much quantity of each item will he need, if he has to make tea for five persons? If two students take 20 minutes to arrange chairs for an assembly, then how much time would five students take to do the same job ? We come across many such situations in our day-to-day life, where we need to see variation in one quantity bringing in variation in the other quantity. For example : (i) If the number of articles purchased increases, the total cost also increases. (ii) More the money deposited in a bank, more is the interest earned. (iii) As the speed of a vehicle increases, the time taken to cover the same distance decreases. (iv) For a given job, more the number of workers, less will be the time taken to complete the work. Observe that change in one quantity leads to change in the other quantity. How do we find out the quantity of each item needed by Mohan? Or, the time five students take to complete the job ? To answer such questions, we now study some concepts of variation. 13.2 DIRECT PROPORTION Consider the following situation. Suppose you go to a grocery shop to buy eggs. If the shopkeeper is selling 2 eggs for Rs. 4, then what amount is required to buy 5 eggs ? We can solve this problem using the unitary method. First, let us determine the cost of 1 egg. It is given that cost of 2 eggs = Rs. 4 so, Cost of 1 egg =  R s .   4 2 = Rs. 2 Hence, cost of 5 eggs = 5 × Rs. 2 = Rs. 10 What do we observe in the above example ? One simple thing that we observe is that as the number of eggs increases, its cost also increases. Such situations are examples of direct proportion. In our day-to-day lives, we come across various such situations. For example, if a car moves with constant speed, then the distance covered by it is in direct proportion with the time taken to cover the distance. Direct proportion can be defined as follows.

Suppose a car uses 4 litres of petrol to travel a distance of 60 km. How far will it travel using 12 litres? The answer is 180 km. How did we calculate it? Since petrol consumed in the second instance is 12 litres, i.e., three times of 4 litres, the distance travelled will also be three times of 60 km. In other words, when the petrol consumption becomes three-fold, the distance travelled is also three fold the previous one. Let the consumption of petrol be x litres and the corresponding distance travelled be y km.

Now, complete the following table :

We find that as the value of x increases, value of y also increases in such a way that the ratio  x y does not change; it remains constant (say k). In this case, it is  1 15 . We say that x and y are in direct proportion, if  x y = k or x = ky. In this example, 4 60 = 12 180 , where 4 and 12 are the quantities of petrol consumed in litres (x) and 60 and 180 are the distances (y) in km. So when x and y are in direct proportion, we can write x 1 y 1 = x 2 y 2  [y 1 , y 2 are values of y corresponding to the values x 1 , x 2 of x respectively] The consumption of petrol and the distance travelled by a car is a case of direct proportion. Similarly, the total amount spent and the number of articles purchased is also an example of direct proportion.  

Suppose variables x and y are in direct proportion. If y 1  and y 2  are the values of y corresponding to the respective values of x 1  and x 2 , then  x 1 y 1 = k and  x 2 y 2 = k . Therefore, we can write the equation as follows: x 1 y 1 = x 2 y 2 Let us now discuss some examples based on this concept. Example 1 . The scale of a map is given as 1 : 10000. The distance between two buildings in a city on the map is 5 cm. What is the actual distance between the two buildings? Solution. Here, the distance on the map and the actual distance between the buildings are in direct proportion. Let the actual distance between the buildings be x. ∴ 1 10000 = 5   c m x ⇒ x = (10000 × 5) cm x = 50000 cm x =  50000 100   m x = 500 m Thus, the actual distance between the buildings is 500 m. Example 2 . If 1 kg 600 g of rice is sufficient for 20 people, then what quantity of rice will be sufficient for 27 people ? Also calculate for how many people 2 kg 400 g of rice will be sufficient. Solution. Let x kg of rice be sufficient for 27 people and 2 kg 400 g of rice be sufficient for y number of people. 1 kg 600 g = 1.6 kg 2 kg 400 g = 2.4 kg The given information can be represented by the following table :

Here, the quantity of rice and the number of people are in direct proportion. ∴ 1 . 6 20 = x 27 and  1 . 6 20 = 2 . 4 y

x = 27 × 1 . 6 20   a n d   y = 2 . 4 × 20 1 . 6 x = 2.16 kg and y = 30 people x = 2 kg 160 g and y = 30 people Hence, 2 kg 160 g of rice will be sufficient for 27 people and 2 kg 400 g of rice will be sufficient for 30 people. Example 3 . A car travels at a constant speed of 35 km/h. How far can it travel in 15 minutes? Solution. Speed of car = 35 km/h This means that the car travels 35 km in 60 minutes. Let the car travel x km in 15 minutes. The given information can be represented by the following table :

Here, the distance covered by the car and the time taken by it are in direct proportion. ∴ 35   k m 60   m i n = x 15   m i n

⇒ x = 35 60 × 15   k m    

⇒ x = 35 4   k m   = 8 . 75   k m Thus, the car travels 8.75 km in 15 minutes. Example 4 . If 12 machines can be assembled in 4 hours, then how many machines can be assembled in 8 hours ? Solution. Let x machines be assembled in 8 hours. The given information can be represented by the following table :

Here, the number of machines and the time taken to assemble them are in direct proportion.

∴ 12 4 = x 8

x = 12 × 8 4

Thus, 24 machines can be assembled in 8 hours. Example 5 . At a particular time of the day, the length of the shadow of a 28 feet high tree is 1.4 feet. Determine the height of a tree that has a shadow of length 2.3 feet at the same time of the day ? Solution. Let the height of the tree having shadow length 2.3 feet at the given time be x feet. The given information can be represented by the following table :

At a particular time of the day, the height of the tree and length of its shadow are in direct proportion.

∴ 28   f t 1 . 4   f t = x 2 . 3   f t

x =   28   ×   2 . 3 1 . 4 f t

x = 46   f t

Hence, the height of the second tree is 46 feet. Example 6 . State whether the given situations involve two variables in direct proportion. 1. Distance covered by a car and the quantity of petrol consumed by it 2. Number of workers and the time taken by them to complete a work 3. Speed of a person and the time taken by him/her to cover a fixed distance 4. Speed of a person and the distance covered by him/her in a fixed time 5. Time period and simple interest if the rate of interest is fixed 6. Time period and rate of interest if the simple interest is fixed 7. Area of cultivated land and the crop harvested Solution. (1) The quantity of petrol consumed by a car increases if the distance covered by it also increases. Thus, the distance covered by a car is in direct proportion with the quantity of petrol consumed by it. (2) More number of workers will take less time to complete a work. Thus, the number of workers and the time taken by them to complete the work are not in direct proportion. (3) If a person travels at a higher speed, then he/she takes less time to cover a fixed distance. Thus, the speed of a person and the time taken by him/her to cover a fixed distance are not in direct proportion. (4) If a person increases his/her speed, then he/she will cover more distance in a fixed time. Hence, the speed of a person and the distance covered by him/her in a fixed time are in direct proportion. (5) For a fixed rate of interest, if the time period is more, then the simple interest will also be more. Hence, the time period and the simple interest are in direct proportion if the rate of interest is fixed. (6) For a fixed simple interest, if the time period is more, then the rate of interest will be less. Hence, the time period and the rate of interest are not in direct proportion if the rate of interest is fixed. (7) The more the area of land cultivated, the more will be the amount of crop harvested. Hence, the area of cultivated land and the crop harvested are in direct proportion. 13.3. VERIFICATION OF DIRECT PROPORTION Consider the following situation : You go to a stationery shop to buy some pens. If each pen costs Rs. 5, then what amount is required to buy 4 such pens? Also, determine the amount you need to pay to buy 10 such pens? It is given that cost of 1 pen = Rs. 5 Hence, cost of 4 pens = 4 × Rs. 5 = Rs. 20 Similarly, cost of 10 pens = 10 × Rs. 5 = Rs. 50 This information can be represented in the table form, where the number of pens is denoted by variable x and their corresponding cost is denoted by variable y, as

If we observe the ratio of the corresponding values of x and y, then we see that 1 5 = 1 5 ; 4 20 = 1 5 ; 10 50 = 1 5 We, thus, observe that as the number of pens (x) increases, their cost (y) also increases in such a manner that their ratio  x y remains constant, say k. Thus, in this case, the value of k is 1 5 . Hence, we say that x and y are in direct proportion, if  x y = k or x = ky Thus, to check whether the variables x and y are in direct proportion, we need to find the ratio  x y for their corresponding values. If this ratio remains constant, then the variables are in direct proportion, otherwise, they are not. Let us now discuss some more examples based on this concept. Example 7 . The following table lists the distance covered by a person and the corresponding time taken by him to cover this distance. Check whether the distance covered changes in direct proportion with the time taken.

Solution. The above information can be represented in a table by taking the distance covered (km) as variable x and the corresponding time taken (minutes) as y.

Thus, we can find the ratio  x y for the corresponding values of x and y as   4 16 = 1 4 ;   6 24 = 1 4 ;   12 48 = 1 4 ; 20 72 = 5 18 Since the ratio x y does not remain constant, the distance covered by the person does not change in direct proportion with the time taken. Example 8 . Observe the following tables and find whether x and y are directly proportional.

Thus, 2 6 = 1 3

14 42 = 1 3

15 45 = 1 3

17 51 = 1 3

19 57 = 1 3

Since the ratio  x y remains constant for the corresponding values of x and y, the variables x and y are directly proportional.

Thus, 50 40 = 5 4

45 36 = 5 4

37 . 5 30 = 5 4

30 24 = 5 4

25 20 = 5 4

5 4 = 5 4 Since the ratio  x y remains constant for the corresponding values of x and y, the variables x and y are directly proportional.

48 38 = 24 19

42 32 = 21 16

39 29 = 39 29

30 20 = 3 2

17 7 = 17 7 Since the ratio  x y does not remain constant for the corresponding values of x and y, the variables x and y are not directly proportional. 13.4. INVERSE PROPORTION Two quantities may change in such a manner that if one quantity increases, the other quantity decreases and vice versa. For example, as the number of workers increases, time taken to finish the job decreases. Similarly, if we increase the speed, the time taken to cover a given distance decreases. To understand this, let us look into the following situation. Zaheeda can go to her school in four different ways. She can walk, run, cycle or go by car. Study the following table.

Observe that as the speed increases, time taken to cover the same distance decreases. As Zaheeda doubles her speed by running, time reduces to half. As she increases her speed to three times by cycling, time decreases to one third. Similarly, as she increases her speed to 15 times, time decreases to one fifteenth. (Or, in other words the ratio by which time decreases is inverse of the ratio by which the corresponding speed increases). Let us consider another example. A school wants to spend Rs. 6000 on mathematics textbooks. How many books could be bought at Rs. 40 each? Clearly 150 books can be bought. If the price of a textbook is more than Rs. 40, then the number of books which could be purchased with the same amount of money would be less than 150. Observe the following table.

Observe that as the price of the books increases, the number of books that can be bought, keeping the fund constant, will decrease. Ratio by which the price of books increases when going from 40 to 50 is 4 : 5, and the ratio by which the corresponding number of books decreases from 150 to 120 is 5 : 4. This means that the two ratios are inverses of each other. Notice that the product of the corresponding values of the two quantities is constant; that is, 40 × 150 = 50 × 120 = 6000. If we represent the price of one book as x and the number of books bought as y, then as x increases y decreases and vice-versa. It is important to note that the product xy remains constant. We say that x varies inversely with y and y varies inversely with x. Thus two quantities x and y are said to vary in inverse proportion if there exists a relation of the type xy = k between them, k being a constant. If y 1 , y 2 are the values of y corresponding to the values x 1 , x 2 of x respectively then x 1 y 1 = x 2 y 2 (= k), or  x 1 x 2 = y 1 y 2 . We say that x and y are in inverse proportion.

Example 9 . In each of the following statements, find the situation where two variables are in inverse proportion. 1. Distance covered by a car and the amount of petrol required 2. Number of workers and time taken by them to complete the work 3. Speed of a person and distance covered by him in a fixed time 4. Length and breadth of a rectangle to keep its area constant Solution. (1) If we want to cover more distance, then we will require more amount of petrol. Hence, distance covered by a car and amount of petrol is in direct proportion, not in inverse proportion. (2) If number of workers will be more, then they will take less time to complete the work. Hence, the number of workers and time taken by them to complete the work are in inverse proportion. (3) If a person will increase his speed, then he will cover more distance in a fixed time. Hence, the speed of a person and distance covered by him in a fixed time are not in inverse proportion. (4) If we will increase the length of rectangle, then we will have to decrease its breadth in order to keep its area constant. Hence, to keep the area of a rectangle constant, its length and breadth should be in inverse proportion. Example 10 . A packet of chocolates is to be distributed among 25 children such that each of them will get 4 chocolates. How many more chocolates would each of them get if the number of children is reduced by 5 ? Solution. Let each child get x more chocolates. Hence, each child will get (4 + x) chocolates. There were 25 children. If number of children is reduced by 5, then there are 25 − 5 = 20 children We can represent the given situation by constructing a table between the number of children and number of chocolates as shown below.

The number of children and the number of chocolates that each child got are in inverse proportion. ∴ 25 × 4 = 20 (4 + x) 4 + x = 25 × 4 20 4 + x = 5 x = 5 − 4 = 1 Therefore, each child will get 1 more chocolate if 5 children are reduced. Example 11 . In one full day in a school, there are 8 periods of 40 min each. The school management decided to increase the number of periods in a day so that more classes can take place in a single day. However, they want to keep the school duration the same. What will be the duration of new periods if the number of periods is increased to 10 ? Solution. Let the duration of new periods be x. The given situation can be represented with the help of the following table.

Here, the number of periods and time duration of each period are in inverse proportion. ∴ 40 × 8 = x × 10 x =  40 × 8 10 = 32 Therefore, the duration of new periods will be 32 minutes. 13.5. VERIFICATION OF INVERSE VARIATION The following table shows the speed of a train and time taken to cover the same distance.

Are the speed of the train and the time taken to cover the distance in inverse proportion? We know that

Therefore, to check whether the two variables x and y of a given situation are in inverse proportion or not, we have to calculate the product of the value of variable x with its corresponding value of the variable y. If all these products are equal, then we can say that the variables x and y are in inverse proportion, otherwise not. Using this concept, let us check whether the speed of train and time taken to cover the distance is in inverse proportion or not. In the given table, there are two variables − speed of the train and time taken to cover the distance. For the first observation, the product of these variables is 20 × 6 = 120. Similarly, for the other observations, the products of corresponding values of the variables are 30 × 4 = 120 40 × 3 = 120 50 × 2.4 = 120 Here, the products of the values of the variables for all observations are the same. Thus, the speed and time taken to cover the same distance are in inverse proportion. Using this concept, we can check whether the variables of a given situation, given in a tabular form, are in inverse proportion or not. Let us discuss one more example based on verification of inverse proportion.   Example 12 . Observe the following tables and check whether x and y are related inversely or not.

Solution. We know that two quantities x and y are in inverse proportion, if x × y = constant. (i) Here, 1 × 20 = 20 2 × 10 = 20 5 × 4 = 20 10 × 2 = 20 It can be seen that x × y = 20, which is constant for each observation. Therefore, x and y are in inverse proportion. (ii) Here, 7 × 27 = 189 8 × 20 = 160 9 × 12 = 108 10 × 7 = 70 It can be seen that x × y is not constant for each observation. Therefore, x and y are not in inverse proportion.

Have a doubt ? Discuss with teachers.

Select Subject Science Maths