problem solving on first law of thermodynamics

• Privacy Policy

Read Chemistry

The first law of thermodynamics + solved problems.

Read Chemistry May 21, 2019 Physical Chemistry

– The first law of Thermodynamics states that The total energy of an isolated system remains constant though it may change from one form to another.

Internal Energy

– A thermodynamic system containing some quantity of matter has within itself a definite quantity of energy.

– This energy includes not only the translation kinetic energy of the molecules but also other molecular energies such as rotational, and vibrational energies.

– The kinetic and potential energy of the nuclei and electrons within the individual molecules also contribute to the energy of the system.

– Internal Energy  is The total of all the possible kinds of energy of a system.

– The word (internal) is often omitted and the energy of a system always implies internal energy.

– The internal energy of a system, like temperature, pressure, volume, etc., is determined by the state of a system and is independent of the path by which it is obtained.

– Hence internal energy of a system is a state function.

– For example, we consider the heating of one mole of liquid water from 0 º to 100 º C.

– The change in energy is 1.8 kcal and is the same regardless of the form in which this energy is transferred to the water by heating, by performing work, by electrical means, or in any other way.

– Since the value of the internal energy of a system depends on the mass of the matter contained in a system, it is classed as an extensive property.

Symbol Representation of Internal Energy and Sign Conventions

– The internal energy of a system is represented by the symbol (E) (Some books use the symbol U).

– It is neither possible nor necessary to calculate the absolute value of the internal energy of a system.

– In thermodynamics, we are concerned only with the energy changes when a system changes from one state to another.

– If ΔE is the difference in energy of the initial state (E in ) and the final state (E f ), we can write

ΔE = E f – E in

 ΔE is +ve if E f is greater than E in

and ΔE is –ve if E f is less than E in .

– A system may transfer energy to or from the surroundings as heat or as work, or both.

Units of Internal Energy

– The SI unit for the internal energy of a system is the joule (J).

– Another unit of energy that is not an SI unit is the calorie, 1 cal = 4.184 J.

The first law of Thermodynamics statement

– The first law of thermodynamics is, in fact, an application of the broad principle known as the Law of Conservation of Energy to the thermodynamic system.

– First law of Thermodynamics states that: The total energy of an isolated system remains constant though it may change from one form to another.

– When a system is changed from state A to state B, it undergoes a change in the internal energy from E A to E B .

– Thus, we can write:

ΔE = E B – E A

– This energy change is brought about by the evolution or absorption of heat and/or by work being done by the system.

– Because the total energy of the system must remain constant, we can write the mathematical statement of the First Law as:

ΔE = q – w            …(1)

– where q = the amount of heat supplied to the system, w = work done by the system

– Thus the First Law may also be stated as the net energy change of a closed system is equal to the heat transferred to the system minus the work done by the system.

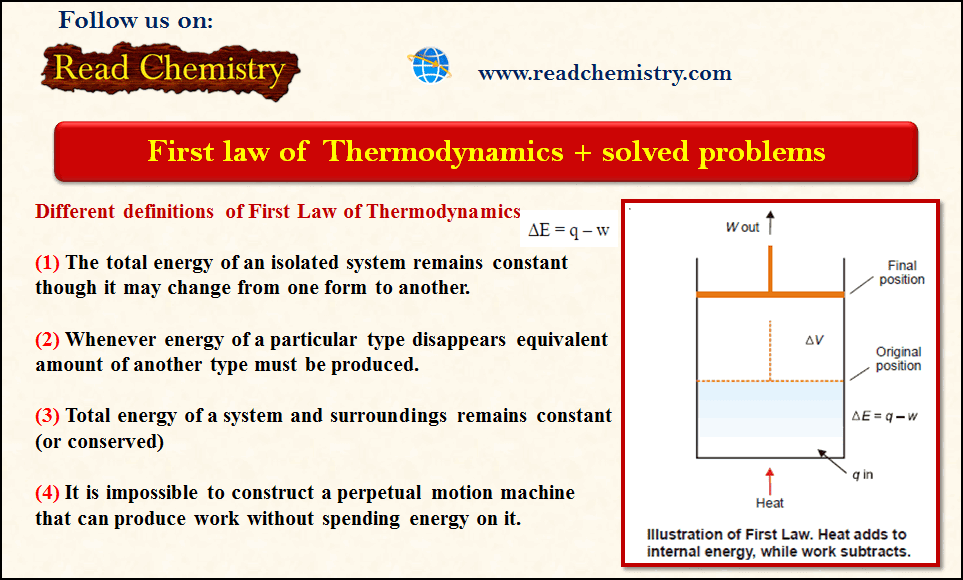
– To illustrate the mathematical statement of the First Law, let us consider the system ‘expanding hot gas’.

– The gas expands against an applied constant pressure by volume ΔV.

– The total mechanical work done is given by the relation:

w = P × ΔV          …(2)

– From (1) and (2), we can restate:

ΔE = q – P × ΔV

Other Definitions of the First Law of Thermodynamics

(1) Whenever energy of a particular type disappears equivalent amount of another type must be produced.

(2) Total energy of a system and surroundings remains constant (or conserved)

(3) It is impossible to construct a perpetual motion machine that can produce work without spending energy on it.

Some Special Forms of the First Law of Thermodynamics

– The mathematical statement of the First Law of Thermodynamics is:

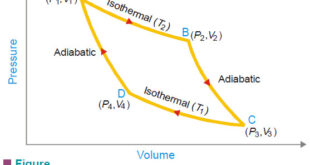
Case (1): For a cyclic process involving isothermal expansion of an ideal gas

Case (2): For an isochoric process (no change in volume) there is no work of expansion i.e. w = 0.

Case (3): For an adiabatic process there is no change in heat gained or lost i.e. q = 0.

– In other words, the decrease in internal energy is exactly equal to the work done on the system by surroundings.

Case (4): For an isobaric process there is no change in pressure, i.e. P remains constant.

or ΔE = q – PΔV

Solved Problem

Problem (1): Find ΔE, q, and w if 2 moles of hydrogen at 3 atm pressure expand isothermally at 50ºC and reversibly to a pressure of 1 atm.

– Since the operation is isothermal and the gas is ideal

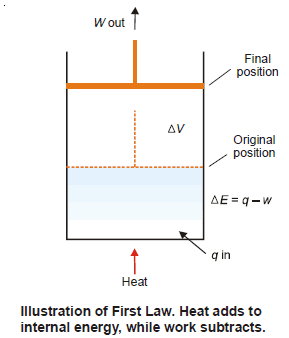
Problem (2): 1g of water at 373 K is converted into steam at the same temperature. The volume of water becomes 1671 ml on boiling. Calculate the change in the internal energy of the system if the heat of vaporization is 540 cal/g.

– As the vaporization takes place against a constant pressure of 1 atmosphere, work done for an irreversible process, w, is:

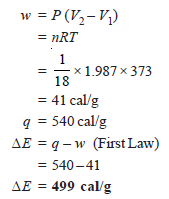
Problem (3): A gas contained in a cylinder fitted with a frictionless piston expands against a constant external pressure of 1 atm from a volume of 5 liters to a volume of 10 liters. In doing so it absorbs 400 J thermal energy from its surroundings. Determine ΔE for the process.

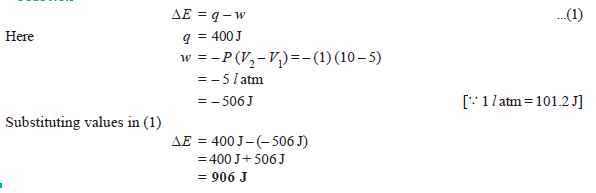
Problem (4): Calculate the maximum work done when pressure on 10 g of hydrogen is reduced from 20 to one atmosphere at a constant temperature of 273 K. The gas behaves ideally. Will there be any change in internal energy? Also, calculate ‘q’.

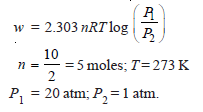
Reference:  Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolor edition.

Related posts:

• Heat of Formation (Definition, Applications, Solved Problems)
• Types of Radiations and its properties
• Difference between Isotopes, Isobar, and Isotones
• Ways of Expressing Concentration
• Laws of Osmotic Pressure
• What is meant by A phase and components?
• Sulphur system – Phase diagram of Sulphur
• How to determine the order of reaction?
• Gels : Defination, Types, Properties

Macromolecules : Definition and Molecular Weight

Related articles.

Gibbs Helmholtz Equations

October 20, 2024

Carnot Cycle – Definition, Theorem, Efficiency, Derivation

May 22, 2024

Entropy : Definition, Units, Solved Problems

May 21, 2024

May 20, 2024

Second Law of Thermodynamics: MCQ Quiz with answers

May 18, 2024

Applications of Colloids

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

About me and why I created this physics website.

Thermodynamics Problems

• Search Website

Real World Applications — for high school level and above

• Amusement Parks
• Battle & Weapons
• Engineering
• Miscellaneous

Education & Theory — for high school level and above

• Useful Formulas
• Physics Questions
• Example Mechanics Problems
• Learn Physics Compendium

Kids Section

• Physics For Kids
• Science Experiments
• Science Fair Ideas
• Science Quiz
• Science Toys
• Teacher Resources
• Commercial Disclosure
• Privacy Policy

© Copyright 2009-2024 real-world-physics-problems.com

Gurumuda Networks

Thermodynamics – problems and solutions

The first law of thermodynamics

1. Based on graph P-V below, what is the ratio of the work done by the gas in the process I, to the work done by the gas in the process II?

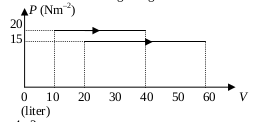
Process 1 :

Pressure (P) = 20 N/m 2

Initial volume (V 1 ) = 10 liter = 10 dm 3 = 10 x 10 -3 m 3

Final volume (V 2 ) = 40 liter = 40 dm 3 = 40 x 10 -3 m 3

Process 2 :

Process (P) = 15 N/m 2

Initial volume (V 1 ) = 20 liter = 20 dm 3 = 20 x 10 -3 m 3

Final volume (V 2 ) = 60 liter = 60 dm 3 = 60 x 10 -3 m 3

Wanted : The ratio of the work done by gas

The work done by gas in the process I :

W = P ΔV = P (V 2 –V 1 ) = (20)(40-10)(10 -3 m 3 ) = (20)(30)(10 -3 m 3 ) = (600)(10 -3 m 3 ) = 0.6 m 3

The work done by gas in the process II :

W = P ΔV = P (V 2 –V 1 ) = (15)(60-20)(10 -3 m 3 ) = (15)(40)(10 -3 m 3 ) = (600)(10 -3 m 3 ) = 0.6 m 3

The ratio of the work done by gas in the process I and the process II :

0.6 m 3 : 0.6 m 3

Based on the graph below, what is the work done by helium gas in the process AB?

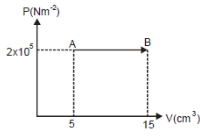
Pressure (P) = 2 x 10 5 N/m 2 = 2 x 10 5 Pascal

Initial volume (V 1 ) = 5 cm 3 = 5 x 10 -6 m 3

Final volume (V 2 ) = 15 cm 3 = 15 x 10 -6 m 3

Wanted : Work done by gas in process AB

W = P (V 2 – V 1 )

W = (2 x 10 5 )(15 x 10 -6 – 5 x 10 -6 )

W = (2 x 10 5 )(10 x 10 -6 ) = (2 x 10 5 )(1 x 10 -5 )

W = 2 Joule

Based on the graph below, what is the work done in process a-b?

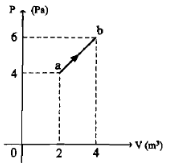
Initial pressure (P 1 ) = 4 Pa = 4 N/m 2

Final pressure (P 2 ) = 6 Pa = 6 N/m 2

Initial volume (V 1 ) = 2 m 3

Final volume (V 2 ) = 4 m 3

Wanted : work done I process a-b

Work done by gas = area under curve a-b

W = area of triangle + area of rectangle

W = ½ (6-4)(4-2) + 4(4-2)

W = ½ (2)(2) + 4(2)

W = 10 Joule

4. Based on graph below, what is the work done in process A-B-C-A.

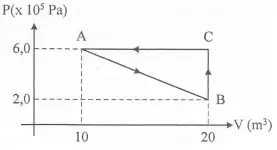
W = ½ (20-10)(6 x 10 5 – 2 x 10 5 )

W = ½ (10)(4 x 10 5 )

W = (5)(4 x 10 5 )

W = 20 x 10 5

W = 2 x 10 6 Joule

Heat engine

5. An engine absorbs 2000 Joule of heat at a high temperature and exhausted 1200 Joule of heat at a low temperature. What is the efficiency of the engine?

Heat input (Q H ) = 2000 Joule

Heat output (Q L ) = 1200 Joule

Work done by engine (W) = 2000 – 1200 = 800 Joule

Wanted : efficiency (e)

e = W / Q H

e = 800/2000

e = 0.4 x 100%

Carnot engine

6. An engine absorbs heat at 960 Kelvin and the engine discharges heat at 576 Kelvin. What is the efficiency of the engine.

High temperature (T H ) = 960 K

Low temperature (T L ) = 576 K

Wanted: efficiency (e)

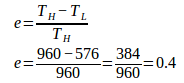
Efficiency of Carnot engine = 0.4 x 100% = 40%

7. Based on the graph below, work done by the engine is 6000 Joule. What is the heat discharged by engine each circle?

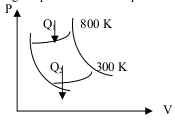
Work (W) = 6000 Joule

High temperature (T H ) = 800 Kelvin

Low temperature (T L ) = 300 Kelvin

Wanted: heat discharged by the engine

Carnot (ideal) efficiency :

Heat absorbed by Carnot engine :

6000 = (0.625) Q 1

Q 1 = 6000 / 0.625

Heat discharged by Carnot engine :

Q 2 = Q 1 – W

Q 2 = 9600 – 6000

Q 2 = 3600 Joule

8. The efficiency of a Carnot engine is 40%. If heat absorbed at 727°C then what is the low temperature.

Efficiency (e) = 40% = 40/100 = 0.4

High temperature (T H ) = 727 o C + 273 = 1000 K

Wanted : Low temperature

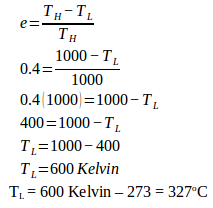
T L = 600 Kelvin – 273 = 327 o C

9. Based on graph below, if the engine absorbs 800 J of heat, what is the work done by the engine.

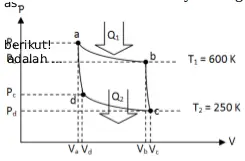
High temperature (T H ) = 600 Kelvin

Low temperature (T L ) = 250 Kelvin

Heat input (Q 1 ) = 800 Joule

Wanted: Work (W)

The efficiency of Carnot engine :

Work was done by the engine :

W = (7/12)(800 Joule)

W = 466.7 Joule

10. The high temperature of a Carnot engine is 600 K. If the engine absorbs 600 J of heat and the low temperature is 400 K, what is the work done by the engine.

Low temperature (T L ) = 400 K

High temperature (T H ) = 600 K

Heat input (Q 1 ) = 600 Joule

Wanted: Work was done by Carnot engine (W)

The efficiency of the Carnot engine :

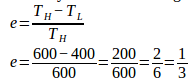
Work was done by Carnot engine :

W = (1/3)(600) = 200 Joule

• What is the primary focus of thermodynamics? Answer : Thermodynamics focuses on the study of energy, its transformations, and its relationship with matter, especially in systems at equilibrium.
• How is the zeroth law of thermodynamics related to temperature? Answer : The zeroth law states that if two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other. This implies the existence of a property called temperature, which is the same for all systems in thermal equilibrium.
• What does the first law of thermodynamics describe? Answer : The first law, also known as the law of energy conservation, states that energy cannot be created or destroyed, only converted from one form to another. In a closed system, the change in internal energy is equal to the heat added to the system minus the work done by the system on its surroundings.
• Why is the second law of thermodynamics crucial for understanding the direction of natural processes? Answer : The second law states that the entropy (or disorder) of an isolated system always increases or remains constant. This dictates that energy spontaneously disperses if not hindered from doing so, providing a direction to natural processes and essentially explaining why certain processes occur spontaneously while others do not.
• What is entropy, and how does it relate to disorder in a system? Answer : Entropy is a measure of the amount of energy in a system that is unavailable to do work. It is also often described as a measure of the system’s disorder or randomness. In general, higher entropy corresponds to greater disorder or randomness.
• How does the third law of thermodynamics describe the entropy of a perfect crystal at absolute zero? Answer : The third law states that the entropy of a perfect crystal is exactly zero at absolute zero temperature (0 Kelvin). This means that at this temperature, the system is perfectly ordered.
• Why can’t heat flow from a colder body to a hotter body on its own? Answer : This behavior is a consequence of the second law of thermodynamics. If heat were to flow from a colder body to a hotter one spontaneously, it would lead to a decrease in the overall entropy of the system, which is not favored by natural processes.
• What is the difference between an isolated, closed, and open system in thermodynamics? Answer : An isolated system does not exchange energy or matter with its surroundings. A closed system can exchange energy but not matter with its surroundings. An open system can exchange both energy and matter with its surroundings.
• How is the concept of “work” in thermodynamics different from the everyday use of the term? Answer : In thermodynamics, “work” refers to the process of energy transfer where forces applied to an object move it in a direction parallel to the force. For example, when a gas expands against a piston, it does work on the piston. This is a more specific definition compared to the everyday use of “work,” which might simply mean any task or activity.

What is a Carnot cycle, and why is it significant in thermodynamics? Answer : The Carnot cycle is an idealized thermodynamic cycle that provides an upper limit on the efficiency that any classical thermodynamic engine can achieve during the conversion of heat into work (or vice versa). It’s significant because it sets a fundamental efficiency limit based on the temperatures of the heat reservoirs between which an engine operates.

Share this:

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 15 Thermodynamics

108 15.1 The First Law of Thermodynamics

• Define the first law of thermodynamics.
• Describe how conservation of energy relates to the first law of thermodynamics.
• Identify instances of the first law of thermodynamics working in everyday situations, including biological metabolism.
• Calculate changes in the internal energy of a system, after accounting for heat transfer and work done.

If we are interested in how heat transfer is converted into doing work, then the conservation of energy principle is important. The first law of thermodynamics applies the conservation of energy principle to systems where heat transfer and doing work are the methods of transferring energy into and out of the system. The first law of thermodynamics states that the change in internal energy of a system equals the net heat transfer into the system minus the net work done by the system. In equation form, the first law of thermodynamics is

Here[latex]\boldsymbol{\Delta{U}}[/latex]is the change in internal energy [latex]\boldsymbol{U}[/latex]of the system.[latex]\boldsymbol{Q}[/latex]is the net heat transferred into the system —that is,[latex]\boldsymbol{Q}[/latex]is the sum of all heat transfer into and out of the system.[latex]\boldsymbol{W}[/latex]is the net work done by the system —that is,[latex]\boldsymbol{W}[/latex]is the sum of all work done on or by the system. We use the following sign conventions: if[latex]\boldsymbol{Q}[/latex]is positive, then there is a net heat transfer into the system; if[latex]\boldsymbol{W}[/latex]is positive, then there is net work done by the system. So positive[latex]\boldsymbol{Q}[/latex]adds energy to the system and positive[latex]\boldsymbol{W}[/latex]takes energy from the system. Thus[latex]\boldsymbol{\Delta{U}=Q-W}.[/latex]Note also that if more heat transfer into the system occurs than work done, the difference is stored as internal energy. Heat engines are a good example of this—heat transfer into them takes place so that they can do work. (See Figure 2 .) We will now examine[latex]\boldsymbol{Q},\:\boldsymbol{W},[/latex]and[latex]\boldsymbol{\Delta{U}}[/latex]further.

MAKING CONNECTIONS: LAW OF THERMODYNAMICS AND LAW OF CONSERVATION OF ENERGY

The first law of thermodynamics is actually the law of conservation of energy stated in a form most useful in thermodynamics. The first law gives the relationship between heat transfer, work done, and the change in internal energy of a system.

Heat Q and Work W

Heat transfer ([latex]\boldsymbol{Q}[/latex]) and doing work ([latex]\boldsymbol{W}[/latex]) are the two everyday means of bringing energy into or taking energy out of a system. The processes are quite different. Heat transfer, a less organized process, is driven by temperature differences. Work, a quite organized process, involves a macroscopic force exerted through a distance. Nevertheless, heat and work can produce identical results. For example, both can cause a temperature increase. Heat transfer into a system, such as when the Sun warms the air in a bicycle tire, can increase its temperature, and so can work done on the system, as when the bicyclist pumps air into the tire. Once the temperature increase has occurred, it is impossible to tell whether it was caused by heat transfer or by doing work. This uncertainty is an important point. Heat transfer and work are both energy in transit—neither is stored as such in a system. However, both can change the internal energy[latex]\boldsymbol{U}[/latex]of a system. Internal energy is a form of energy completely different from either heat or work.

Internal Energy U

We can think about the internal energy of a system in two different but consistent ways. The first is the atomic and molecular view, which examines the system on the atomic and molecular scale. The internal energy [latex]\boldsymbol{U}[/latex]of a system is the sum of the kinetic and potential energies of its atoms and molecules. Recall that kinetic plus potential energy is called mechanical energy. Thus internal energy is the sum of atomic and molecular mechanical energy. Because it is impossible to keep track of all individual atoms and molecules, we must deal with averages and distributions. A second way to view the internal energy of a system is in terms of its macroscopic characteristics, which are very similar to atomic and molecular average values.

Macroscopically, we define the change in internal energy[latex]\boldsymbol{\Delta{U}}[/latex]to be that given by the first law of thermodynamics:

Many detailed experiments have verified that[latex]\boldsymbol{\Delta{U}=Q-W},[/latex]where[latex]\boldsymbol{\Delta{U}}[/latex]is the change in total kinetic and potential energy of all atoms and molecules in a system. It has also been determined experimentally that the internal energy[latex]\boldsymbol{U}[/latex]of a system depends only on the state of the system and not how it reached that state . More specifically,[latex]\boldsymbol{U}[/latex]is found to be a function of a few macroscopic quantities (pressure, volume, and temperature, for example), independent of past history such as whether there has been heat transfer or work done. This independence means that if we know the state of a system, we can calculate changes in its internal energy[latex]\boldsymbol{U}[/latex]from a few macroscopic variables.

MAKING CONNECTIONS: MACROSCOPIC AND MICROSCOPIC

In thermodynamics, we often use the macroscopic picture when making calculations of how a system behaves, while the atomic and molecular picture gives underlying explanations in terms of averages and distributions. We shall see this again in later sections of this chapter. For example, in the topic of entropy, calculations will be made using the atomic and molecular view.

To get a better idea of how to think about the internal energy of a system, let us examine a system going from State 1 to State 2. The system has internal energy[latex]\boldsymbol{U_1}[/latex]in State 1, and it has internal energy[latex]\boldsymbol{U_2}[/latex]in State 2, no matter how it got to either state. So the change in internal energy[latex]\boldsymbol{\Delta{U}=U_2-U_1}[/latex]is independent of what caused the change. In other words,[latex]\boldsymbol{\Delta{U}}[/latex] is independent of path . By path, we mean the method of getting from the starting point to the ending point. Why is this independence important? Note that[latex]\boldsymbol{\Delta{U}=Q-W}.[/latex]Both[latex]\boldsymbol{Q}[/latex]and[latex]\boldsymbol{W}[/latex] depend on path , but[latex]\boldsymbol{\Delta{U}}[/latex]does not. This path independence means that internal energy[latex]\boldsymbol{U}[/latex]is easier to consider than either heat transfer or work done.

Example 1: Calculating Change in Internal Energy: The Same Change in U is Produced by Two Different Processes

(a) Suppose there is heat transfer of 40.00 J to a system, while the system does 10.00 J of work. Later, there is heat transfer of 25.00 J out of the system while 4.00 J of work is done on the system. What is the net change in internal energy of the system?

(b) What is the change in internal energy of a system when a total of 150.00 J of heat transfer occurs out of (from) the system and 159.00 J of work is done on the system? (See Figure 3 ).

In part (a), we must first find the net heat transfer and net work done from the given information. Then the first law of thermodynamics[latex]\boldsymbol{(\Delta{U}=Q-W)}[/latex]can be used to find the change in internal energy. In part (b), the net heat transfer and work done are given, so the equation can be used directly.

Solution for (a)

The net heat transfer is the heat transfer into the system minus the heat transfer out of the system, or

Similarly, the total work is the work done by the system minus the work done on the system, or

Thus the change in internal energy is given by the first law of thermodynamics:

We can also find the change in internal energy for each of the two steps. First, consider 40.00 J of heat transfer in and 10.00 J of work out, or

Now consider 25.00 J of heat transfer out and 4.00 J of work in, or

The total change is the sum of these two steps, or

Discussion on (a)

No matter whether you look at the overall process or break it into steps, the change in internal energy is the same.

Solution for (b)

Here the net heat transfer and total work are given directly to be[latex]\boldsymbol{Q=-150.00\textbf{ J}}[/latex]and[latex]\boldsymbol{W=-159.00\textbf{ J}},[/latex]so that

Discussion on (b)

A very different process in part (b) produces the same 9.00-J change in internal energy as in part (a). Note that the change in the system in both parts is related to[latex]\boldsymbol{\Delta{U}}[/latex]and not to the individual[latex]\boldsymbol{Q}\text{s}[/latex]or[latex]\boldsymbol{W}\text{s}[/latex]involved. The system ends up in the same state in both (a) and (b). Parts (a) and (b) present two different paths for the system to follow between the same starting and ending points, and the change in internal energy for each is the same—it is independent of path.

Human Metabolism and the First Law of Thermodynamics

Human metabolism is the conversion of food into heat transfer, work, and stored fat. Metabolism is an interesting example of the first law of thermodynamics in action. We now take another look at these topics via the first law of thermodynamics. Considering the body as the system of interest, we can use the first law to examine heat transfer, doing work, and internal energy in activities ranging from sleep to heavy exercise. What are some of the major characteristics of heat transfer, doing work, and energy in the body? For one, body temperature is normally kept constant by heat transfer to the surroundings. This means[latex]\boldsymbol{Q}[/latex]is negative. Another fact is that the body usually does work on the outside world. This means[latex]\boldsymbol{W}[/latex]is positive. In such situations, then, the body loses internal energy, since[latex]\boldsymbol{\Delta{U}=Q-W}[/latex]is negative.

Now consider the effects of eating. Eating increases the internal energy of the body by adding chemical potential energy (this is an unromantic view of a good steak). The body metabolizes all the food we consume. Basically, metabolism is an oxidation process in which the chemical potential energy of food is released. This implies that food input is in the form of work. Food energy is reported in a special unit, known as the Calorie. This energy is measured by burning food in a calorimeter, which is how the units are determined.

In chemistry and biochemistry, one calorie (spelled with a lowercase c) is defined as the energy (or heat transfer) required to raise the temperature of one gram of pure water by one degree Celsius. Nutritionists and weight-watchers tend to use the dietary calorie, which is frequently called a Calorie (spelled with a capital C). One food Calorie is the energy needed to raise the temperature of one kilogram of water by one degree Celsius. This means that one dietary Calorie is equal to one kilocalorie for the chemist, and one must be careful to avoid confusion between the two.

Again, consider the internal energy the body has lost. There are three places this internal energy can go—to heat transfer, to doing work, and to stored fat (a tiny fraction also goes to cell repair and growth). Heat transfer and doing work take internal energy out of the body, and food puts it back. If you eat just the right amount of food, then your average internal energy remains constant. Whatever you lose to heat transfer and doing work is replaced by food, so that, in the long run,[latex]\boldsymbol{\Delta{U}=0}.[/latex]If you overeat repeatedly, then[latex]\boldsymbol{\Delta{U}}[/latex]is always positive, and your body stores this extra internal energy as fat. The reverse is true if you eat too little. If[latex]\boldsymbol{\Delta{U}}[/latex]is negative for a few days, then the body metabolizes its own fat to maintain body temperature and do work that takes energy from the body. This process is how dieting produces weight loss.

Life is not always this simple, as any dieter knows. The body stores fat or metabolizes it only if energy intake changes for a period of several days. Once you have been on a major diet, the next one is less successful because your body alters the way it responds to low energy intake. Your basal metabolic rate (BMR) is the rate at which food is converted into heat transfer and work done while the body is at complete rest. The body adjusts its basal metabolic rate to partially compensate for over-eating or under-eating. The body will decrease the metabolic rate rather than eliminate its own fat to replace lost food intake. You will chill more easily and feel less energetic as a result of the lower metabolic rate, and you will not lose weight as fast as before. Exercise helps to lose weight, because it produces both heat transfer from your body and work, and raises your metabolic rate even when you are at rest. Weight loss is also aided by the quite low efficiency of the body in converting internal energy to work, so that the loss of internal energy resulting from doing work is much greater than the work done. It should be noted, however, that living systems are not in thermal equilibrium.

The body provides us with an excellent indication that many thermodynamic processes are irreversible . An irreversible process can go in one direction but not the reverse, under a given set of conditions. For example, although body fat can be converted to do work and produce heat transfer, work done on the body and heat transfer into it cannot be converted to body fat. Otherwise, we could skip lunch by sunning ourselves or by walking down stairs. Another example of an irreversible thermodynamic process is photosynthesis. This process is the intake of one form of energy—light—by plants and its conversion to chemical potential energy. Both applications of the first law of thermodynamics are illustrated in Figure 4 . One great advantage of conservation laws such as the first law of thermodynamics is that they accurately describe the beginning and ending points of complex processes, such as metabolism and photosynthesis, without regard to the complications in between. Table 1 presents a summary of terms relevant to the first law of thermodynamics.

Section Summary

• The first law of thermodynamics is given as[latex]\boldsymbol{\Delta{U}=Q-W},[/latex]where[latex]\boldsymbol{\Delta{U}}[/latex]is the change in internal energy of a system,[latex]\boldsymbol{Q}[/latex]is the net heat transfer (the sum of all heat transfer into and out of the system), and[latex]\boldsymbol{W}[/latex]is the net work done (the sum of all work done on or by the system).
• Both[latex]\boldsymbol{Q}[/latex]and[latex]\boldsymbol{W}[/latex]are energy in transit; only[latex]\boldsymbol{\Delta{U}}[/latex] represents an independent quantity capable of being stored.
• The internal energy[latex]\boldsymbol{U}[/latex]of a system depends only on the state of the system and not how it reached that state.
• Metabolism of living organisms, and photosynthesis of plants, are specialized types of heat transfer, doing work, and internal energy of systems.

Conceptual Questions

1: Describe the photo of the tea kettle at the beginning of this section in terms of heat transfer, work done, and internal energy. How is heat being transferred? What is the work done and what is doing it? How does the kettle maintain its internal energy?

2: The first law of thermodynamics and the conservation of energy, as discussed in Chapter 7.6 Conservation of Energy , are clearly related. How do they differ in the types of energy considered?

3: Heat transfer[latex]\boldsymbol{Q}[/latex]and work done[latex]\boldsymbol{W}[/latex]are always energy in transit, whereas internal energy[latex]\boldsymbol{U}[/latex]is energy stored in a system. Give an example of each type of energy, and state specifically how it is either in transit or resides in a system.

4: How do heat transfer and internal energy differ? In particular, which can be stored as such in a system and which cannot?

5: If you run down some stairs and stop, what happens to your kinetic energy and your initial gravitational potential energy?

6: Give an explanation of how food energy (calories) can be viewed as molecular potential energy (consistent with the atomic and molecular definition of internal energy).

7: Identify the type of energy transferred to your body in each of the following as either internal energy, heat transfer, or doing work: (a) basking in sunlight; (b) eating food; (c) riding an elevator to a higher floor.

Problems & Exercises

1: What is the change in internal energy of a car if you put 12.0 gal of gasoline into its tank? The energy content of gasoline is[latex]\boldsymbol{1.3\times10^8\textbf{ J/gal}}.[/latex]All other factors, such as the car’s temperature, are constant.

2: How much heat transfer occurs from a system, if its internal energy decreased by 150 J while it was doing 30.0 J of work?

3: A system does[latex]\boldsymbol{1.80\times10^8\textbf{ J}}[/latex]of work while[latex]\boldsymbol{7.50\times10^8\textbf{ J}}[/latex]of heat transfer occurs to the environment. What is the change in internal energy of the system assuming no other changes (such as in temperature or by the addition of fuel)?

4: What is the change in internal energy of a system which does[latex]\boldsymbol{4.50\times10^5\textbf{ J}}[/latex]of work while[latex]\boldsymbol{3.00\times10^6\textbf{ J}}[/latex]of heat transfer occurs into the system, and[latex]\boldsymbol{8.00\times10^6\textbf{ J}}[/latex]of heat transfer occurs to the environment?

5: Suppose a woman does 500 J of work and 9500 J of heat transfer occurs into the environment in the process. (a) What is the decrease in her internal energy, assuming no change in temperature or consumption of food? (That is, there is no other energy transfer.) (b) What is her efficiency?

6: (a) How much food energy will a man metabolize in the process of doing 35.0 kJ of work with an efficiency of 5.00%? (b) How much heat transfer occurs to the environment to keep his temperature constant? Explicitly show how you follow the steps in the Problem-Solving Strategy for thermodynamics found in Chapter 15.5 Problem-Solving Strategies for Thermodynamics .

7: (a) What is the average metabolic rate in watts of a man who metabolizes 10,500 kJ of food energy in one day? (b) What is the maximum amount of work in joules he can do without breaking down fat, assuming a maximum efficiency of 20.0%? (c) Compare his work output with the daily output of a 187-W (0.250-horsepower) motor.

8: (a) How long will the energy in a 1470-kJ (350-kcal) cup of yogurt last in a woman doing work at the rate of 150 W with an efficiency of 20.0% (such as in leisurely climbing stairs)? (b) Does the time found in part (a) imply that it is easy to consume more food energy than you can reasonably expect to work off with exercise?

9: (a) A woman climbing the Washington Monument metabolizes[latex]\boldsymbol{6.00\times10^2\textbf{ kJ}}[/latex]of food energy. If her efficiency is 18.0%, how much heat transfer occurs to the environment to keep her temperature constant? (b) Discuss the amount of heat transfer found in (a). Is it consistent with the fact that you quickly warm up when exercising?

[latex]\boldsymbol{1.6\times10^9\textbf{ J}}[/latex]

[latex]\boldsymbol{-9.30\times10^8\textbf{ J}}[/latex]

(a)[latex]\boldsymbol{-1.0\times10^4\textbf{ J}},[/latex]or[latex]\boldsymbol{-2.39\textbf{ kcal}}[/latex]

(b)[latex]\boldsymbol{2.10\times10^6\textbf{ J}}[/latex]

(c) Work done by the motor is[latex]\boldsymbol{1.61\times10^7\textbf{ J}}[/latex];thus the motor produces 7.67 times the work done by the man

(b) This amount of heat is consistent with the fact that you warm quickly when exercising. Since the body is inefficient, the excess heat produced must be dissipated through sweating, breathing, etc.

College Physics: OpenStax Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book